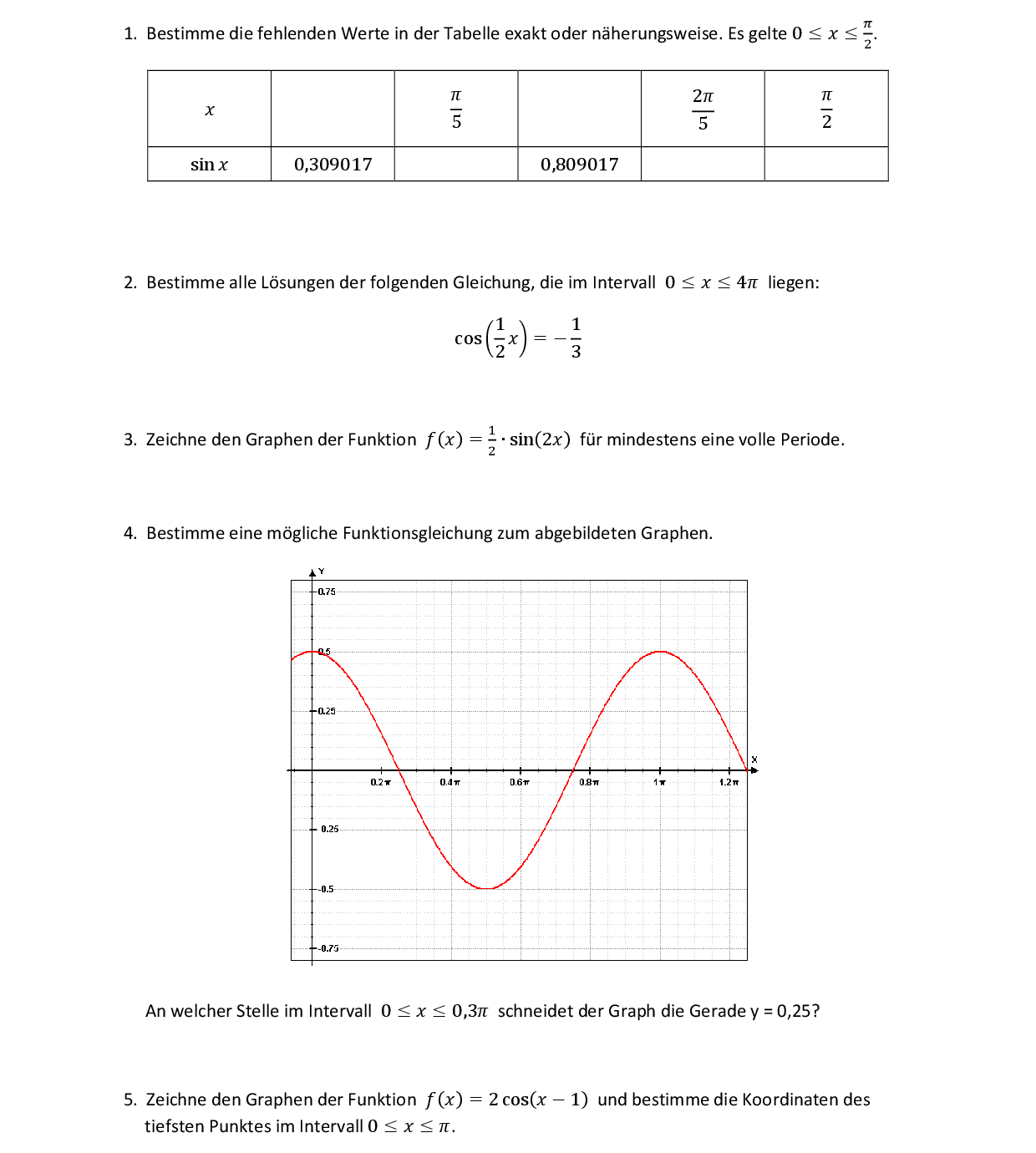
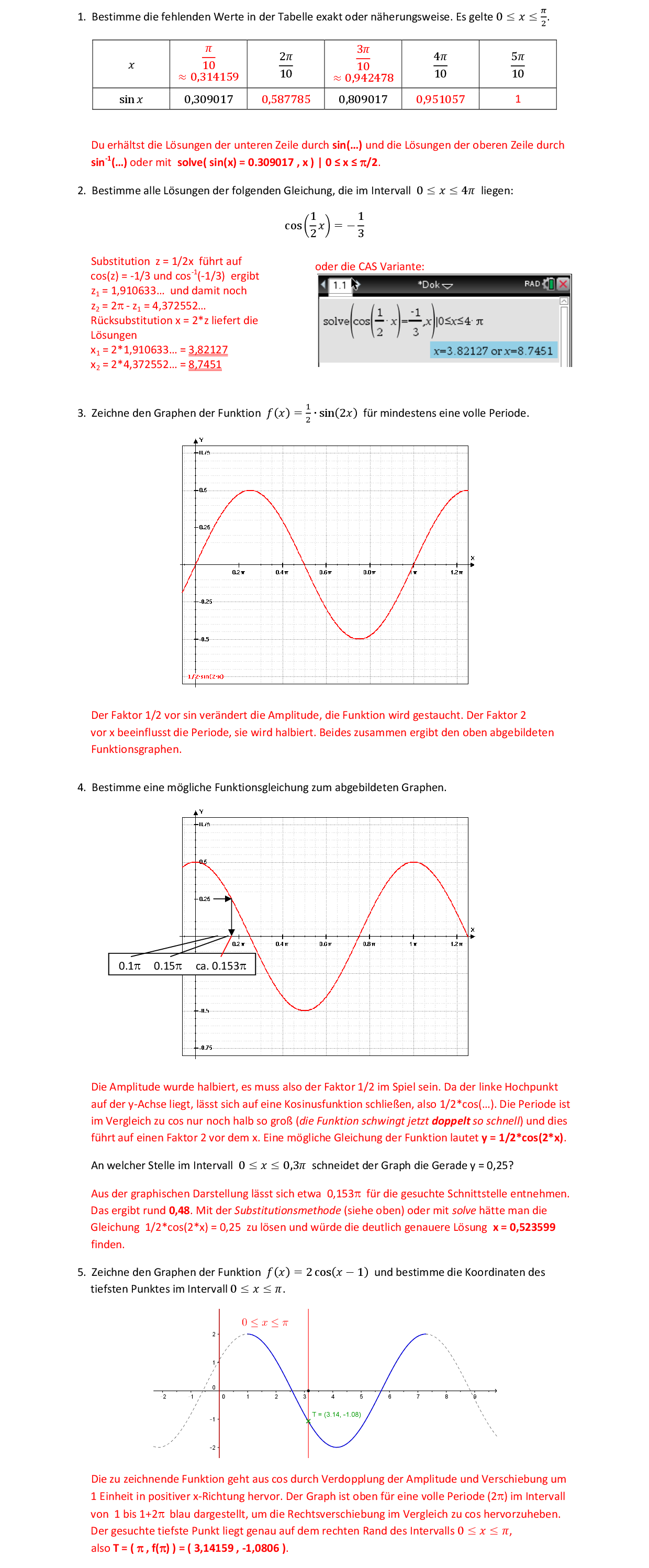
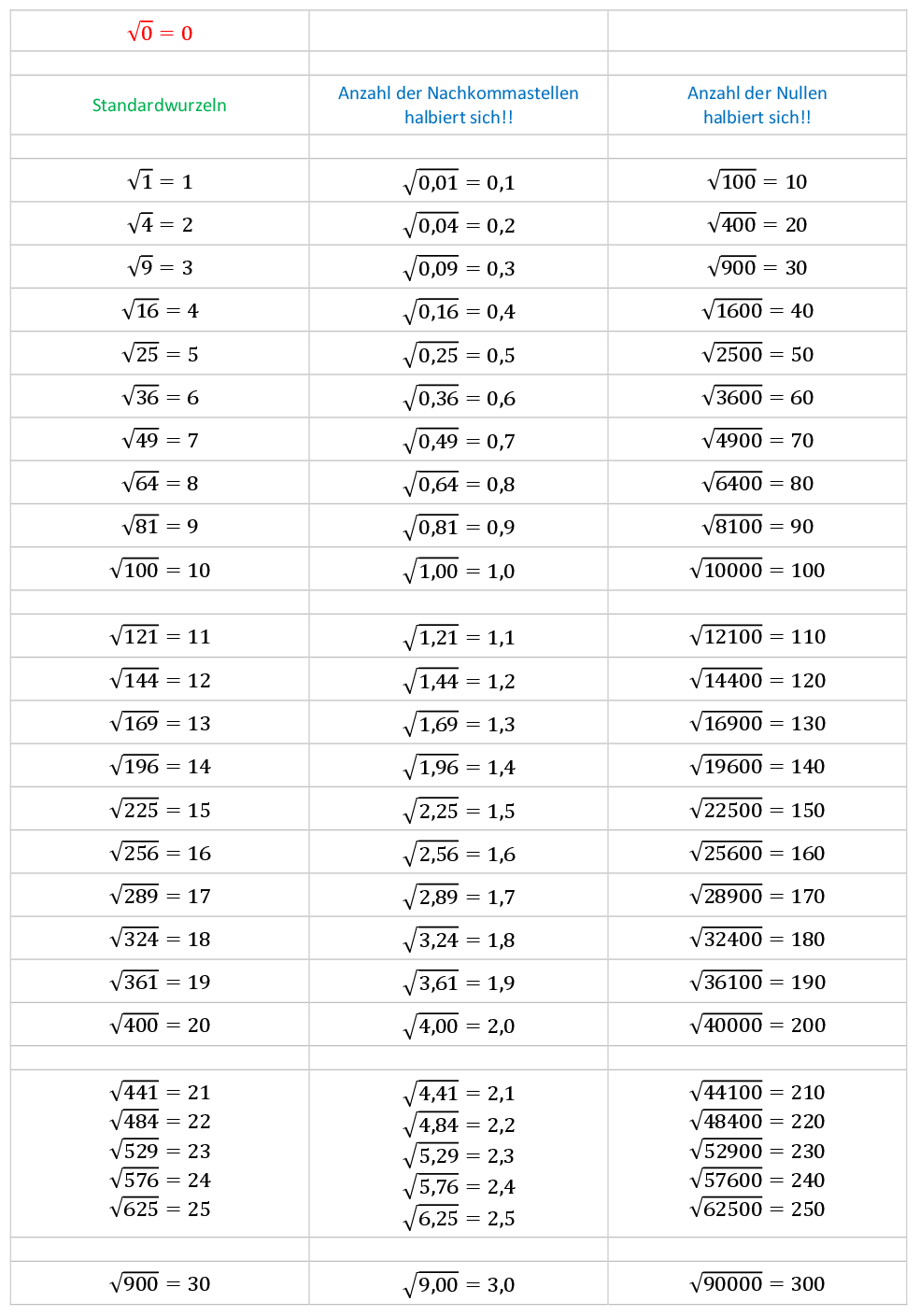
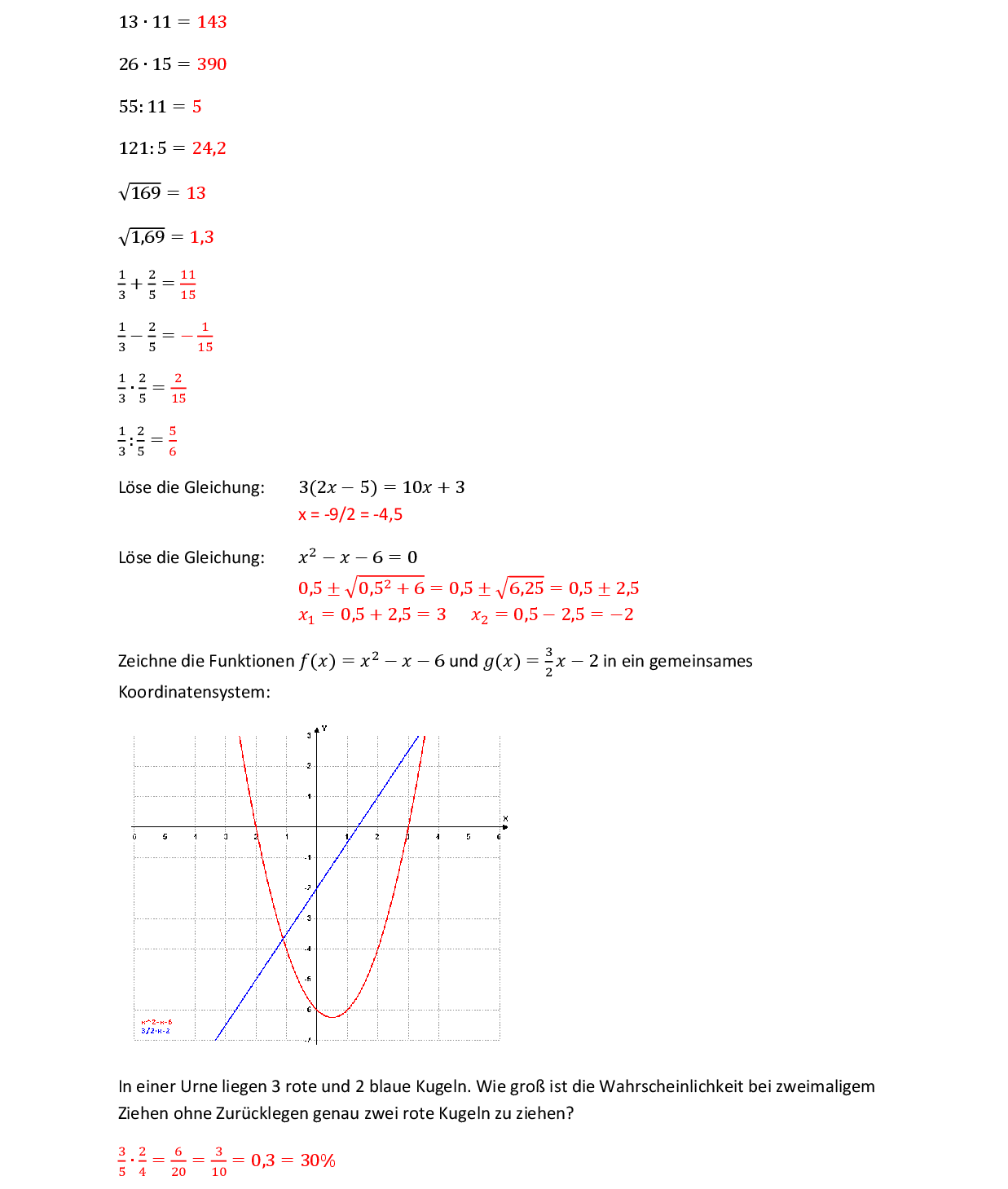
Am Kreis können Radius, Durchmesser, Umfang und Flächeninhalt mit den folgenden Formeln berechnet werden:
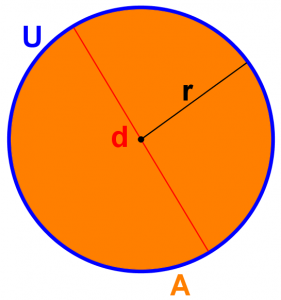Umfang U = 2 * π * r = π * d
Fläche/Flächeninhalt A = π * r2 = π * d2 / 4
Radius r = d / 2
bzw.
Durchmesser d = 2 * r.
Ist der Umfang eines Kreises gegeben, so berechnet man zunächst am schnellsten den Durchmesser mit der Formel
d = U / π.
Ist die Fläche eines Kreises gegeben, dann lässt sich am einfachsten als erstes der Radius berechen
r = √(A / π)
Mit den folgenden Aufgaben kann die richtige Verwendung der Formeln trainiert werden. Die Lösungen folgen direkt im Anschluss.
Aufgaben:
Berechne für den jeweiligen Kreis die fehlenden Größen Radius, Durchmesser, Umfang oder Flächeninhalt.
| r | 6 cm | 12,3 m | ||
| d | 4 m | 1,2 km | ||
| U | ||||
| A | ||||
| r | ||||
| d | ||||
| U | 16 cm | 3,14 m | ||
| A | 20 cm2 | 3,45 m2 |
Lösungen der ersten Tabelle:
d = 6 cm * 2 = 12 cm U = π * 12 cm = 37,70 cm A = π * (6 cm)2 = 113,10 cm2
d = 12,3 m * 2 = 24,6 m U = π * 24,6 m = 77,28 m A = π * (12,3 m)2 = 475,29 m2
r = 4 m / 2 = 2 m U = π * 4 m = 12,57 m A = π * (2 m)2 = 12,57 m2
r = 1,2 km / 2 = 0,6 km U = π * 1,2 km = 3,77 km A = π * (0,6 km)2 = 1,13 km2
| r | 6 cm | 12,3 m | 2 m | 0,6 km |
| d | 12 cm | 24,6 m | 4 m | 1,2 km |
| U | 37,70 cm | 77,28 m | 12,57 m | 3,77 km |
| A | 113,10 cm2 | 475,29 m2 | 12,57 m2 | 1,13 km2 |
Lösungen der zweiten Tabelle:
d = 16 cm / π = 5,09 cm r = 5,09 cm / 2 = 2,55 cm A = π * (2,55 cm)2 = 20,43 cm2
d = 3,14 m / π = 1,00 m r = 1,00 m / 2 = 0,50 m A = π * (0,50 m)2 = 0,79 m2
r = √(20 cm2 / π) = 2,52 cm d = 2,52 cm * 2 = 5,04 cm U = π * 5,04 cm = 15,83 cm
r = √(3,45 m2 / π) = 1,05 m d = 1,05 m * 2 = 2,10 m U = π * 2,10 m = 6,60 m
| r | 2,55 cm | 0,50 m | 2,52 cm | 1,05 m |
| d | 5,09 cm | 1,00 m | 5,04 cm | 2,10 m |
| U | 16 cm | 3,14 m | 15,83 cm | 6,60 m |
| A | 20,43 cm2 | 0,79 m2 | 20 cm2 | 3,45 m2 |
